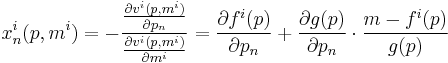Gorman polar form

Gorman polar form is a functional form for indirect utility functions in economics. Imposing this form on utility allows the researcher to treat a society of utility-maximizers as if it consisted of a single 'representative' individual. W. M. Gorman showed that having the function take Gorman polar form is both a necessary and sufficient for this condition to hold.

1 Motivation
2 Definition
3 Proof of linearity and equality of slope of Engel curves
4 Application
5 References
6 See also

Motivation

Early results by Antonelli (1886) and Nataf (1953) had shown that, assuming all individuals face the same prices in a market, their income consumption curves and their Engel curves should be parallel straight lines. Gorman's first published paper in 1953 developed these ideas in order to answer the question of generalizing a society to a single individual.

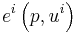In 1961, Gorman published a short, four-page paper in Metroeconomica which derived an explicit expression for the functional form of preferences which give rise to linear Engel curves. Briefly, an individual's ( $i$ ) resulting expenditure function ( $e ^ i \left ( p , u ^ i \right )$ ) must be affine with respect to utility ( $u$ ):

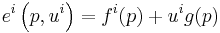$e^i \left (p,u^i \right ) = f^i(p) %2B u^i g(p)$ ,

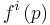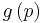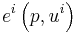where both $f^i \left (p \right )$ and $g \left (p \right )$ are homogeneous of degree one in prices ( $p$ , a vector). This homogeneity condition is trivial, as otherwise $e^i \left (p,u^i \right )$ would not give linear Engel curves.

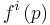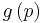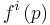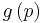$f^i \left (p \right )$ and $g \left (p \right )$ have nice interpretations: $f^i \left (p \right )$ is the expenditure needed to reach a reference utility level of zero for each individual ( $i$ ), while $g \left (p \right )$ is the price index which deflates the excess money income 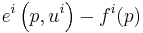$e^i \left (p,u^i \right ) - f^i (p)$ needed to attain a level of utility 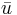$\bar{u}$ . It is important to note that 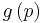$g \left (p \right )$ is the same for every individual in a society.

Definition

Inverting this formula gives the indirect utility function

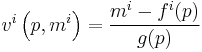$v^i \left (p,m^i \right ) = \frac {m^i-f^i(p)}{g(p)}$ ,

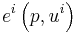where $m$ is the amount of income available to the individual and is equivalent to the expenditure ( $e^i \left (p,u^i \right )$ ) in the previous equation. This is what Gorman called “the polar form of the underlying utility function.” Gorman's use of the term polar was in reference to the idea that the indirect utility function can be seen as using polar rather than Cartesian (as in direct utility functions) coordinates to describe the indifference curve. Here, income ( 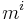$m^i$ ) is analogous to the radius and prices ( $p$ ) to an angle.

Proof of linearity and equality of slope of Engel curves

To prove that the Engel curves of a function in Gorman polar form are linear, apply Roy's identity to the utility function to get a Marshallian demand function for an individual ( $i$ ) and a good ( $n$ ):

$x^i_n(p,m^i) = -\frac{\frac{\partial v^i(p,m^i)}{\partial p_n}}{\frac{\partial v^i(p,m^i)}{\partial m^i}} = \frac{\partial f^i(p)}{\partial p_n} %2B \frac{\partial g(p)}{\partial p_n}\cdot\frac{m-f^i(p)}{g(p)}$

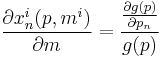This is linear in income ( $m$ ), so the change in an individual's demand for some commodity with respect to a change in that individual's income, $\frac{\partial x^i_n(p,m^i)}{\partial m} = \frac{\frac{\partial g(p)}{\partial p_n}}{g(p)}$ , does not depend on income, and thus Engel curves are linear.

Also, since this change does not depend on variables particular to any individual, the slopes of the Engel curves of different individuals are equal.

Application

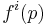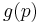Many applications of Gorman polar form are summarized in various texts and in Honohan and Neary's article cited at the end of this article. These applications include the ease of estimation of $f^i(p)$ and $g(p)$ in certain cases. But the most important application is for the theorist of economics, in that it allows a researcher to treat a society of utility-maximizing individuals as a single individual. In other words, under these conditions a community indifference mapping is guaranteed to exist.

References

Honohan, Patrick, and Neary, J Peter. W. M. Gorman (1923–2003). The Economic and Social Review, Vol. 34, No. 2, Summer/Autumn, 2003, pp. 195–209 [1]
W. M. Gorman. On a class of preference fields, Metroeconomica, 13, August 1961, 53-56.
Antonelli, G. B., 1886. Sulla Teoria Matematica dell’Economia Politica, Pisa; English translation in J.S. Chipman, L. Hurwicz, M. K. Richter and H. F. Sonnenschein (eds.): Preferences, Utility and Demand: A Minnesota Symposium, New York: Harcourt Brace Jovanovich, 1971, pp. 333–360.
Nataf, A., 1953. “Sur des questions d’agrégation en économétrie,” Publications de l’Institut de Statistique de l’Université de Paris, 2, Fasc. Vol. 4, pp. 5–61.